Example 2.1: Finite Dimensional Matrices

In this example we consider the system of ordinary differential equations

$u_t + A u = 0, \qquad u(0) = u_0,$

where the matrix A has complex eigenvalues. To avoid these eigenvalues, we split A into two submatrices A1 and A2 that each have only real eigenvalues and compute an approximate solution based on the operator splitting:

$u_t \approx [ \exp(-\Delta t A_2) \circ \exp(-\Delta t A_1) ]^n u_0.$

Show the matrix and compute eigenvalues

A=[1 2; -2 2]
[R, lambda]=eig(A);
disp('Eigenvalues of A:'), disp(diag(lambda)')

A =

     1     2
    -2     2

Eigenvalues of A:
   1.5000 - 1.9365i   1.5000 + 1.9365i

Split A into A1 and A2

Make a splitting so that the eigenvalues of the two new matrices are real

A1 = [0.5 0; -2 1]
[R,lambda1]=eig(A1); disp('Eigenvalues of A1:'), disp(diag(lambda1)')

A2 = A-A1
[R,lambda2]=eig(A2); disp('Eigenvalues of A2:'), disp(diag(lambda2)')

A1 =

    0.5000         0
   -2.0000    1.0000

Eigenvalues of A1:
    1.0000    0.5000


A2 =

    0.5000    2.0000
         0    1.0000

Eigenvalues of A2:
    0.5000    1.0000

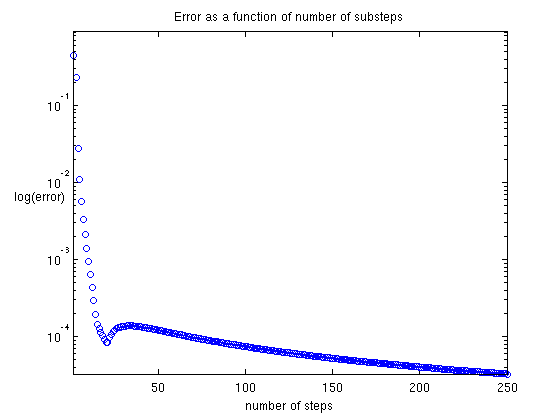
Investigate accuracy of the splitting

We compute the approximate solution at time T=pi using N splitting steps and report the splitting error as a function of N

T=pi;
N=250;
u0=[1 1]';
uexact=expm(-T*A)*u0;
error=zeros(N,1);
for nstep=1:N,
	usplit=u0;
	dt=T/nstep;
	Astep=expm(-dt*A2)*expm(-dt*A1);
	for i=1:nstep;
		usplit=Astep*usplit;
	end;
	error(nstep)=sum(abs(uexact-usplit));
end;

semilogy(error,'o');
title('Error as a function of number of substeps'); axis tight;
ylabel('log(error)','Rotation',0); xlabel('number of steps');