Example A.1: Linear Advection in a Periodic Domain

The linear advection problem with periodic boundary conditions

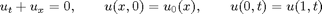
$u_t + u_x = 0, \qquad u(x,0)=u_0(x), \qquad u(0,t)=u(1,t)$

is well suited for studying error mechanisms in numerical schemes for hyperbolic conservation laws. In particular, to study dissipative and oscillatory errors, we will use initial data consisting of a combination of a smooth, squared cosine wave and double step function.

We consider two first-order methods (Lax-Friedrichs and the upwind method) and two second-order methods (Lax-Wendroff and MacCormack)

T  = 10;
N  = 100; h=1/N; x=h*(1:N);
u0 = (abs(x-.25)<=0.15).*(cos(pi*(10/3)*(x-0.25))).^2 + ...
   1.0*(abs(x-0.75)<0.15);
xx  = linspace(0,1,1001);
uf  = (abs(xx-.25)<=0.15).*(cos(pi*(10/3)*(xx-0.25))).^2 + ...
   1.0*(abs(xx-0.75)<0.15);

method = {'LxF', 'upwind', 'LxW', 'McC'};
name   = {'Lax-Friedrichs', 'Upwind', 'Lax-Wendroff', 'MacCormack'};
for i=1:4
   u=finvol('linearfunc',u0,T,h,1,'periodic',method{i},.9);
   subplot(2,2,i);
   plot(xx,uf,'-',x,u,'o','MarkerSize',2); axis([0 1 -0.2 1.3]);
   title(name{i});
end

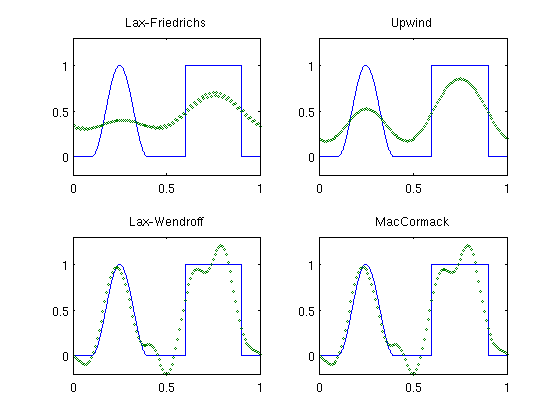
We see that the two first-order schemes smear both the smooth part and the discontinuous path of the advected profile and that the Lax-Friedrichs method is more diffusive than the upwind method. The second-order schemes, on the other hand, preserve the smooth profile quite accurately, but introduce spurious oscillations around the two discontinuities.