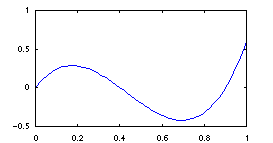
 Figure 1: The flux function in Example 1. |
Dimensional splitting, or sometimes called fractional steps, was first introduced by Godunov[1] in connection with gas dynamics. Consider the following two dimensional equation
Let S(t) denote the entropy solution of (1), and let Sf(t) and Sg(t) denote the entropy solutions of the one-dimensional equationsut + f(u)x + g(u)y = 0, u(x,y,0) = u0(x,y). (1)
Godunov proposed the following approximation to the entropy solutionvt + f(v)x = 0, v(x,0)=v0(x),
wt + g(w)y = 0, w(y,0)=w0(y).
This approximation is formally first order for smooth solutions. Strang [2] showed how to increase the accuracy to second order for smooth solutions by using the alternative approximationu(t)=S(t)u0 ~ [ Sg(dt) Sf(dt)]n u0. (2)
These two methods (2) and (3) are so-called semi-discrete methods, in that the solution operators Sf and Sg are exact.u(t) = S(t)u0 ~ [ Sf(dt/2) Sg(dt) Sf(dt/2)]n u0. (3)
The dimensional splitting scheme can also be used for numerical computations, and it is indeed a natural way to extend one dimensional methods to two or more dimensions. This is realized by approximating the solution operators by some numerical scheme. Observe that Strang's method can be simplified as follows
and hence requires approximately as much work as the Godunov splitting.u(t) = S(t)u0 ~ Sf(dt/2) Sg(dt) [Sf(dt) Sg(dt) ]n-1 Sf(dt/2) u0,
Crandall and Majda [3] proved that both splitting formulas (2) and (3) produce a sequence of approximations that converges to the unique entropy solution as temporal and spatial discretization tends to zero for several numerical schemes (monotone shemes, Lax-Wendroff and Glimm's scheme). When computing discontinuous solutions, the first order accuracy of Godunov's splitting method and the second order accuracy of Strang's now longer holds.
Dimensional splitting can be combined with front tracking to extend this method to arbitrary space dimension. This was first proposed by Holden and Risebro [4]. They showed that the corresponding numerical method is unconditionally stable, i.e., that there is no restriction on the time step. Lie, Haugse and Hvistendahl Karlsen [5] proved that the L1-error of the method is of order 1/2 in time and space.
The one-dimensional front tracking method needs no grid, except when specifying the piecewise constant initial approximation. However, when extended to multidimensions, an underlying grid is introduced to obtain piecewise constant data in one direction from the solution computed in the other. Assume therefore that we have a regular (but not necessarily uniform) Cartesian grid. Let P denote the projection onto the grid. Then the Godunov splitting method (2) based on front tracking reads,
where the solution operators Sf(dt) and Sg(dt) now use the piecewise linear approximations to f and g, respectively.u(t)=S(t)u0 ~ [P Sg(dt) P Sf(dt)]n P u0.
The corresponding numerical method is unconditionally stable in the sense that there is no CFL condition restricting the time step used in each spatial direction. In practise, however, CFL numbers in the range 10 to 20 can be used with surprisingly low loss in accuracy. See [5] for more details. This makes the method very efficient compared to most finite difference or finite volume methods.
For problems with a velocity field
we can define a similar method based upon the front tracking method for problems with variable coefficients. This is discussed in [6].ut + U(x,t)f(u)x + V(x,t)g(u)y=0,
Example 1. In this example we wish to illustrate how the method approximates the solution. Consider therefore the two-dimensional problem (1) with flux functions f(u)=g(u)=10*u*(u-0.4)*(u-0.9), as shown in Figure 1. The initial data is equal 1.0 for x>0.2 and y>0.2 and zero elsewhere. The grid consits of 20 blocks in each direction. We use 40 linear segments in the flux approximation. The splitting time step is 0.05, correspoinding to a CFL number around 7.0.
 Figure 1: The flux function in Example 1. |
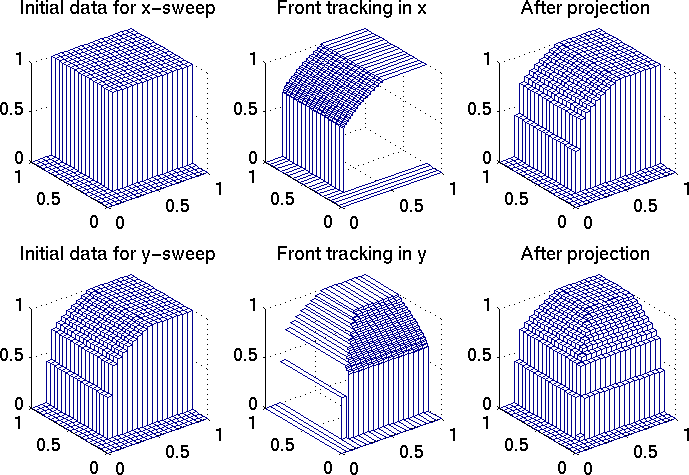 Figure 2: Step number one -- time 0.0 to 0.05. |
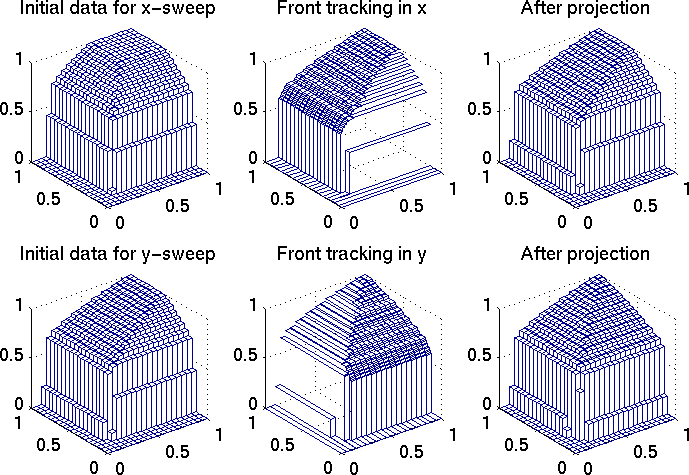 Figure 3: Step number two -- time 0.05 to 0.1. |
with initial data equal 1.0 and -1.0 inside two circles with radius 0.4 centred at (-0.5,-0.5) and (0.5,0.5), respectively, and equal zero elsewhere. The two cylinders will deform and start to move towards the origin. The leading wave of each cylinder is a shock. The two shocks interact and merge into a single, stationary shock aligned with the line x=-y. Figure 4 show the solution at time t=0.6 computed on a 50*50 grid. In the right plot, we have used 30 time steps, corresponding to Godunovs method, whereas 3 steps are used in the middle plot (CFL number around 5). In the left plot, we show a fine grid reference solution. A MPEG-movie shows the solution up to time t=1.0.ut + (0.5u2)x + (0.5u2)x=0,
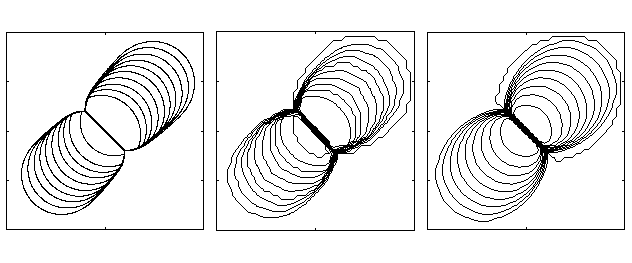 Figure 4: Example 2. Reference solution (left) and solution on a 50*50 grid using 3 time steps (middle) and 30 time steps (right). |