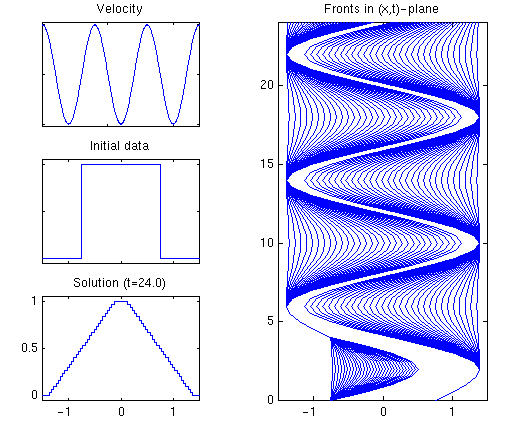
 Figure 1: Example 1. |
The front tracking construction can easily be extended to first-order, quasilinear equations with variable coefficients of the form
The key observation is that the form of the discontinuity paths is not essential in the front tracking method. Assume for the moment that V=V(x)>0. Then the permissible discontinuities for are the same as those for the scalar conservation law. This follows from the Oleinik entropy condition. Consider again the Riemann problemut + V(x,t) f(u)x = 0, u(x,0) = u0(x). (1)
and let fc denote the correct envelope of the flux function. Then the solution consists of constant states separated by discontinuitiesu0(x) = uL, for x < 0
u0(x) = uR, for x > 0
where each path of discontinuity is given by
u(x,t) = u1= uL, for x < x1(t) u(x,t) = ui, for xi-1(t) < x < xi(t), i=2,...,N-1 u(x,t) = uN= uR, for x > xN-1(t)
A similar construction holds if V(x) is negative, but then with the roles of upper and lower convex envelope interchanged in the definition of the envelope function.x'i(t) = V(x) * [fc(ui+1) -fc(ui)]/ [ui+1-ui] = V(x)* si, x(0)=0. (2)
If the velocity V(x) has a simple form, e.g., V(x)=ax+b, the ordinary differential equation (2) can be solved explicitly. In this case, the shock path is given by
Hence, by using a piecewise linear approximation to the velocity field V(x), the discontinuity paths can be computed explicitly. Then the front tracking method follows immediately as in the scalar case. Note that the velocity field may be discontinuous, as long as the sign is preserved over the discontinuity. The same construction can be applied if V=V(t). If V depends both on x and t, one can for instance use a piecewise linear approximation in x and a piecewise constant approximation in t. A more thorough discussion of this method is given in [1].x(t) = (x0 + b/a) exp[ a s(t - t0)] - b/a.
The discretization parameters have been chosen very coarse with purpose in the examples below to clearly demonstrate the nature of the front tracking approximation.
Example 1. Burgers' equation with a time-dependent velocity field
Initially, the solution consists of a shock wave propagating in the positive direction, followed by a rarefaction wave, see Figure 1. At time t=2.0, the velocity changes sign and the shock is transformed to a rarefaction wave which propagates backwards. The initial rarefaction wave becomes steeper and eventually turns into a shock. At time t=6.0, the velocity changes sign again. After this time, the solution consists of two rarefaction waves propagating back and forth. A MPEG-movie shows the solution up to time t=24.0 and GIF image shows the solution in the (x,t)-plane.ut + cos(pi*t/4.0) * (0.5u2)x = 0, u(x,0) = I[-0.75,0.75](x).
 Figure 1: Example 1. |
Example 2. In the next example we introduce x-dependence in the velocity field,
Figure 2 shows the velocity field, initial data, solution at time t=24.0, and fronts in the (x,t)-plane. A MPEG-movie shows the dynamics of the problem and GIF image shows the solution in the (x,t)-plane.ut + cos(pi*(x-t)/4.0) * (0.5u2)x = 0, u(x,0) = I[-0.5,0.5](x).
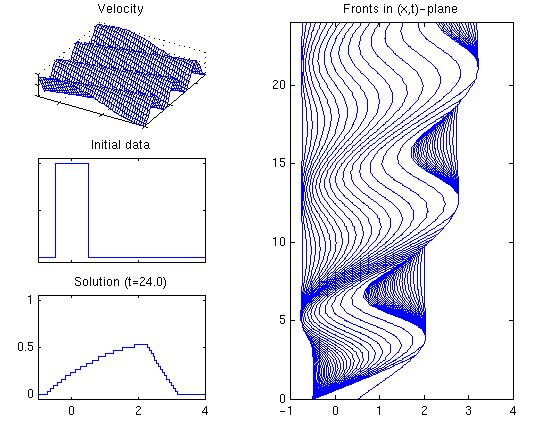 Figure 2: Example 2. |
Example 3. In the final example we consider a non-convex flux function and non-monotone initial data. That is, we wish to solve
Figure 3 shows the solution at time t=3.5 and the tracked discontinuities in the (x,t)-plane. At the left and right boundary we have imposed outflow boundary conditions.ut + 0.75*sin(0.5*pi*x) * [4u2(1-u2)]x = 0, u(x,0) = I[5,5](x)*sin(pi*x).
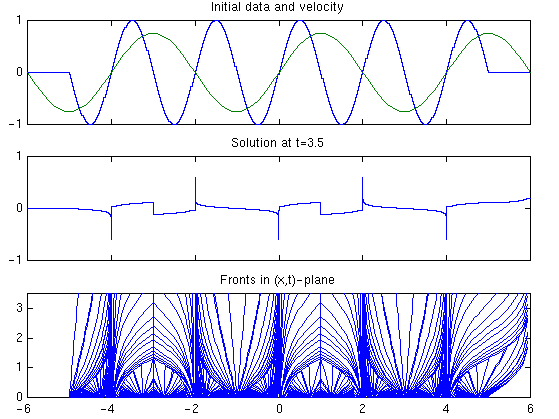 Figure 3: Example 3. |