A Cylindrical Explosion Problem
Front Tracking for the Euler Equations of Gas Dynamics
|
Problems with cylindrical symmetry are good test examples for Cartesian grid methods, since a reliable numerical solution can easily be computed for the equivalent one-dimensional inhomogeneous problem. The following test case has been proposed in E. F. Toro, Riemann solvers and numerical methods for fluid dynamics, Springer, 1997. Consider a square domain [-1,1]x[-1,1]. The initial data are constant in two regions separated by a circle of radius 0.4 centred at the origin. Inside the circle the pressure and density are both 1.0, and outside the density is 0.125 and the pressure equal 0.1. The velocities are zero everywhere. The solution consits of a circular shock wave propagating outwards from the origin, followed by a circular contact discontinuity propagating in the same direction, and a circular rarefaction wave travelling towards the origin. |
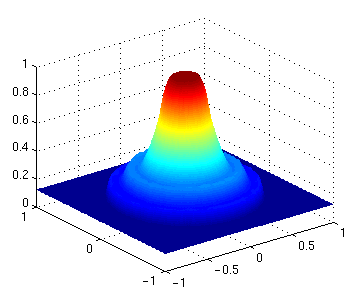 The pressure at time t=0.20 |
 Solution at time t=0.2 |
|
The figure above shows a comparison between the one-dimensional radial reference solution (blue line) and a scatterplot of the solution on a 101x101 grid using 10 time steps. This corresponds to a CFL number in the range 1.2 to 2.2. The shock wave is resolved sharply within two grid points and the contact discontinuity by three points. As expected, the symmetry is not preserved perfectly. |
Knut-Andreas Lie <andreas@math.ntnu.no> Last modified: Fri Mar 20 09:12:22 1998